고정 헤더 영역
상세 컨텐츠
본문
2차 방정식을 쉽게 풀 수 있는 방법으로 근의 공식이라는 것이 있는데요. 오늘은 근의 공식이 어떤 것이고 어떻게 나왔는지 알아보고 실제 문제를 풀때 어떻게 적용하는지 알아보도록 하겠습니다.

근의 공식
a, b, c 가 상수이고 a 가 영이 아닌 경우에 2차 방정식은 아래처럼 일반식으로 표현할 수 있습니다.

이때 근의 공식으로 x 값을 구할 수 있는데요. 그 공식은 바로 아래와 같습니다.

정말 간단합니다. 그렇다면 이 근의 공식을 이용해서 문제를 한번 풀어보도록 하겠습니다.
문제 풀이 적용

위에 있는 2차 방정식을 인수분해서 x 값을 구하면 x = 1 / 2 와 x = -3 이 나오는데요. 인수분해를 하지 않고 근의공식에 바로 대입하도록 하겠습니다. 여기서 a = 2, b = 7, c = 3이기 때문에 그대로 공식에 대입하면

입니다. 이를 계산하면,
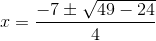
루트를 정리하면,
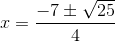
25는 5의 제곱이기 때문에 루트를 제거할 수 있습니다.

여기서 +와 - 를 각각 적용하면 2개의 x값이 나오게 됩니다.

근의 공식을 알고 있으면, a, b, c 값에 바로 적용하면 더하기 빼기 곱하기 나누기만 알면 복잡한 과정 없이 방정식의 해를 구할 수 있습니다.
정리
근의 공식을 이용하면 쉽게 2차 방정식의 해를 구할 수 있습니다. 하지만 루트안에 값이 음수가 되는 경우 실근이 아닌 허근이 나오게 됩니다. 그리고 루트안에 값이 0이 나오게 되는 경우에는 중근이 나오게 됩니다.
일반적으로 허근인 경우에는 해가 없다고 생각하시면 됩니다.
여기서 실근이란 실수로만 이루어진 근을 말하고, 허근이란 허수로만 이루어진 근을 말합니다. 또 중근은 2개의 해가 같은 경우를 의미합니다. 이 2차 방정식을 그래프로도 표현이 가능한데요.

라는 2차 방정식이 있을때 y 가 0인 경우, 즉 직교 좌표계에서 x축과 접하는 지점이 방정식의 해입니다.
서로 다른 2개의 실근인 경우, a 가 양수인 경우에는

과 같은 형태의 그래프가 나오고, a 가 음수인 경우에는

과 같은 형태의 그래프가 나오게 됩니다.
그리고 중근의 경우에는 x축과 딱 만나게 됩니다. 그래프는 아래와 같습니다.


왼쪽은 a가 양수인 경우, 오른쪽은 a가 음수인 경우입니다.
마지막으로 서로 다른 두 허근을 갖는 경우에는 x축과 만나는 점이 없습니다.


어느정도 개념만 이해하고 있다면, 문제를 풀때는 공식을 최대한 활용하는 것이 좋습니다. 시간도 절약되고 하지만 그 원리는 잘 이해하고 고민하는 시간은 꼭 필요해요.
'공부 > 컴퓨터 그래픽 , 수학, 기하학' 카테고리의 다른 글
| 원과 직선이 만나는 점 찾기 (2) | 2020.01.25 |
|---|---|
| 한점에서 직선까지 거리 구하는 공식 (0) | 2020.01.22 |
| 수 체계에 대해서 알아보자. (0) | 2020.01.21 |
| 삼각형 넓이 구하는 공식 (with 헤론의 공식) (0) | 2019.12.26 |





댓글 영역