고정 헤더 영역
상세 컨텐츠
본문
오늘은 기하학에서 꽤 많이 사용하는 한점에서 직선까지의 거리를 구하는 공식에 대해서 알아보도록 하겠습니다. 앞으로 소개할 방법은 총 2가지인데요. 첫번째 방법은 벡터를 이용한 방법, 두번째 방법은 방정식을 이용한 방법입니다. 각 상황에 맞게 사용하면 되니까. 둘다 알고 있으면 도움이 될 것입니다.
1. 벡터를 이용한 방법
벡터를 이용한 방법에서 직선은 2개의 점으로 표현할 수 있습니다. 한 점을 a라고 하고 다른 한점을 b라고 하겠습니다. 그러면 다음과 같이 표현할 수 있습니다.

이때 직선의 벡터를 구할 수 있는데요. 점 a에서 b로 향하는 벡터는 아래와 같습니다.

이때 이 벡터를 90도 회전한 벡터를 구할 수 있는데요. 쉽게 구하기 위해서 x와 y를 바꾸고 y에 -1 을 곱하면 됩니다. 사실 여기에는 행렬을 곱하는 비밀이 있는데요. 이 내용은 다른 포스팅에서 다루기로 하고 일단 이렇게만 기억하시면 됩니다.
그렇다면 예를 들어보겠습니다. 한점이 (0, 1) 이고 다른 한점이 (3, 4)인 경우 직선과 이 직선을 90도 회전한 벡터를 표현한 그림은 아래와 같습니다.

여기까지 이해가 가셨다면 절반정도 이해하신건데요. 이제 직선에서 길이를 구할 점에 대해서 이야기를 하도록 하겠습니다. 해당 점을 P라고 하겠습니다. 그러면 점 P와 90도 회전한 벡터를 이용해서 직선을 만들 수 있습니다.

그렇게 되면 두 직선의 교점을 찾을 수 있고 해당 교점에서 P까지의 거리를 구하게 되면 한점(P)에서 직선까지의 거리를 구할 수 있게 됩니다. 이 방법은 별도의 방정식이 필요없고 곱하기 더하기 빼기 정도만 사용하는 방법이기 때문에 직관적이고 쉽게 구할 수 있는 장점이 있습니다.
2. 방정식을 이용한 방법
다음으로 살펴볼 방법은 방정식을 이용한 방법인데요. 이 방법은 직선의 방정식이 필요합니다. 일반적으로 직선의 방정식은 다음과 같이 표현할 수 있습니다.
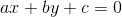
그리고 거리를 구할 점을 P라고 하고 다음과 같이 표현할 수 있습니다.

마지막으로 교점을 I 라고 하면 다음과 같이 표현할 수 있습니다.

이것을 그림으로 표현하면 아래와 같습니다.

우선 시간이 부족하여 결과부터 궁금하신 분들을 위해서 정답부터 알려드리겠습니다.
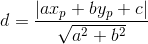
거리를 d라고 하면 다음과 같이 표현할 수 있습니다.
그렇다면 증명을 하기 위해서는 방정식의 해를 구하는 방법을 알야합니다. 결론적으로 직선의 방정식인 ax + by + c = 0과 점 P와 점 I로 만들어지는 새로운 직선의 교점을 구하고 그 교점에서 P까지 거리를 구하는것입니다.
이때 미리 정의한 점 I를 직선의 방정식에 대입하고 점 P와 I의 기울기와 직선의 기울기를 곱하면 -1이 나온다는 것을 이용해서 점 P를 구하는 것입니다. 어떻게보면 방정식을 이용했다는 것을 제외하고 1번의 방법과 많이 유사하다는 것을 알 수 있습니다.
그렇다면 직선의 방정식의 기울기를 구해보도록 하겠습니다. 해당 직선을 y를 제외하고 나머지를 우변으로 이항하고 b로 나누면 다음과 같은 방정식이 됩니다.

여기서 - a / b가 기울기가 되고,
점 P와 I를 이용해서 기울기를 구하면, 기울기는 Y증가량 / X증가량 이므로

이 둘을 곱하면 -1 이 나오게 됩니다.
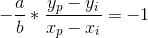
분모를 양쪽에 곱하면 다음과 같습니다.

이때 직선의 방정식에 점 I가 있기 때문에 x, y에 점 I를 넣을 수 있습니다.

이제 미지수가 2개이고 방정식이 2개가 나왔습니다. 따라서 이를 이용해 값을 구할 수 있게 됩니다.
결론적으로 여기서 기억할 것은

이 식만 기억하면 문제를 푸는데는 전혀 문제가 없겠죠? ㅋㅋ
'공부 > 컴퓨터 그래픽 , 수학, 기하학' 카테고리의 다른 글
| 근의 공식에 대해서 알아보자! 문제 풀이 적용 (0) | 2020.04.03 |
|---|---|
| 원과 직선이 만나는 점 찾기 (2) | 2020.01.25 |
| 수 체계에 대해서 알아보자. (0) | 2020.01.21 |
| 삼각형 넓이 구하는 공식 (with 헤론의 공식) (0) | 2019.12.26 |





댓글 영역